基于CART算法的回归树简介

maths & statistics

作者

zenggyu

发布于

2018-04-09

摘要

介绍基于CART的回归树的基本原理。

模型表达式

考虑一个回归问题，记结局为 $y$ ，特征集为 $x$ 。基于CART算法的回归树通过递归二分裂，划分出一系列特征空间 $R_{1}, . . ., R_{m}$ ，并使用下式对结局进行预测：

$y = f (x) = \sum_{k = 1}^{m} I (x \in R_{k}) \times c_{k} (1)$

其中 $c_{k}$ 为常数，是特征空间 $R_{k}$ 内所有观察单位的结局的均值¹。表达式 $x \in R_{k}$ 用于判断观察单位是否位于特征空间 $R_{k}$ 中，当结果为真时， $I (x \in R_{k})$ 取1，否则取0。

¹ 数学上可以证明，当该常数为观察单位结局的均值时，预测误差最小。

递归二分裂

CART算法的基本步骤可以简述如下。首先，遍历当前数据集中所有特征的所有取值，寻找一个最优的变量-取值组合作为分裂点（选取规则请见下节介绍），划分出两个特征空间。然后，分别对位于不同空间的数据子集重复前述过程，直至满足某终止条件（例如：当前空间内的样本量低于特定阈值，或当前空间分裂后某子空间中的样本量低于特定阈值，或分裂已达一定深度等）。

特征空间的划分方式与特征的类型有关，但每次划分所形成的子空间均为两个，因此称递归二分裂。对于一个定量特征或有序定性特征，所有小于或等于所选分裂点的取值形成一个特征空间，而所有大于该分裂点的取值则形成另一个空间。对二分类或无序多分类的定性特征²，取其中一个取值形成一个子空间，其余多个取值则合并成另一个空间（在实际计算中，可以通过设置由各取值形成的多个0-1哑变量实现）。

² 另一种形式是将其中某些取值定义为一个子空间，剩余取值定义为另一个子空间。常见的策略是按某种规则对分类变量的取值进行排序（例如，按分类取值对观察单位进行分组，然后按各组中结局变量的均值大小进行排序），然后选择切分点将其分为两组。当某些分类能够较好地预测结局时，这种方式或可提高模型的预测准确性，但也将使模型更加复杂且难以解释。

以下描述给出了对两个定量特征 $x_{1}$ 和 $x_{2}$ 进行空间划分的具体步骤示例：

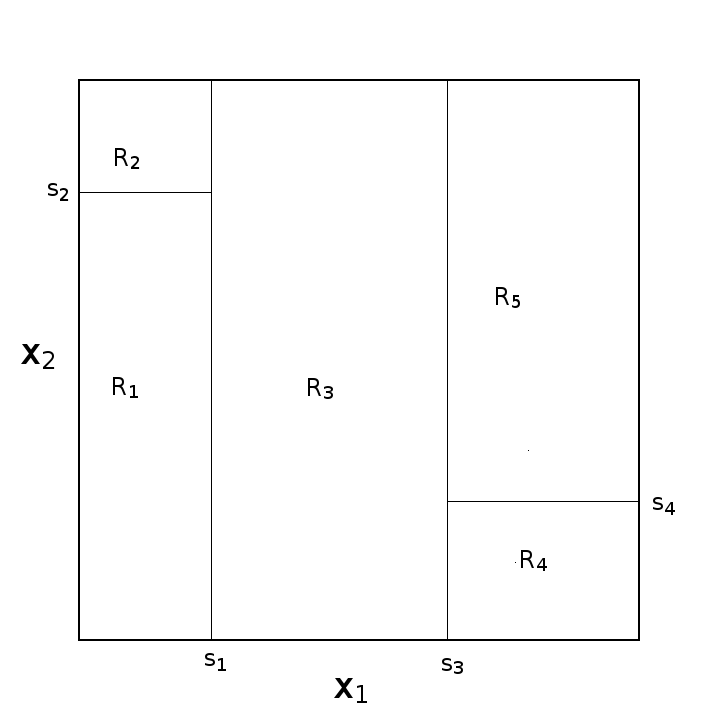
首次划分对原始特征空间 $(x_{1}, x_{2})$ 进行，若选定的分裂点为 $x_{1} = s_{1}$ ，则由此形成以下两个子空间：
- ${(x_{1}, x_{2}) | x_{1} \leq s_{1}}$ 。假设其所含样本量大于等于阈值，则进一步对其进行划分。若选定的分裂点为 $x_{2} = s_{2}$ ，则由此形成以下两个子空间：
  - ${(x_{1}, x_{2}) | x_{1} \leq s_{1}, x_{2} \leq s_{2}}$ 。假设其所含样本量小于阈值，则不再对其进行划分。该空间可记为 $R_{1}$ 。
  - ${(x_{1}, x_{2}) | x_{1} \leq s_{1}, x_{2} > s_{2}}$ 。假设其所含样本量小于阈值，则不再对其进行划分。该空间可记为 $R_{2}$ 。
- ${(x_{1}, x_{2}) | x_{1} > s_{1}}$ 。假设其所含样本量大于等于阈值，则进一步对其进行划分。若选定的分裂点为 $x_{1} = s_{3}$ ，则由此形成以下两个子空间：
  - ${(x_{1}, x_{2}) | x_{1} > s_{1}, x_{1} \leq s_{3}}$ 。假设其所含样本量小于阈值，则不再对其进行划分。该空间可记为 $R_{3}$ 。
  - ${(x_{1}, x_{2}) | x_{1} > s_{3}}$ 。假设其所含样本量大于等于阈值，则进一步对其进行划分。若选定的分裂点为 $x_{2} = s_{4}$ ，则由此形成以下两个子空间：
    - ${(x_{1}, x_{2}) | x_{1} > s_{3}, x_{2} \leq s_{4}}$ 。假设其所含样本量小于阈值，则不再对其进行划分。该空间可记为 $R_{4}$ 。
    - ${(x_{1}, x_{2}) | x_{1} > s_{3}, x_{2} > s_{4}}$ 。假设其所含样本量小于阈值，则不再对其进行划分。该空间可记为 $R_{5}$ 。

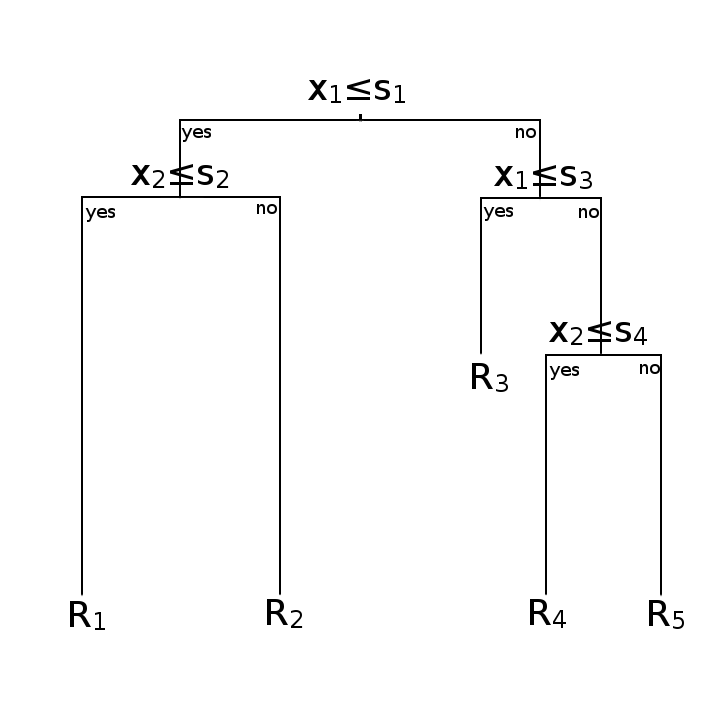
图 1 显示了根据上述步骤进行划分后的结果；图 2 则以树状图的形式对上述过程进行了描绘。在基于树的机器学习算法中，以术语“节点”表示上述特征空间；特别地，原始特征空间被称为“根节点”，不可继续划分的子空间则被称为“叶节点”，而在划分过程中所形成的其余各空间则被称为“内部节点”。一棵树包含一个根节点、若干个内部节点和若干个叶节点，每个节点均包含一个数据子集，且对应一个特征测试。

分裂点的选取

在处理回归问题时，CART算法使用均方误差MSE(Mean Squared Error)来衡量节点的不纯度；MSE越大，不纯度越高。CART算法的优化目标就是降低节点的不纯度。具体地说，若将某个父节点记为 $R_{k}$ ，再记其分裂后的两个子节点为 $R_{k l}$ 和 $R_{k r}$ ；则该算法所选择的分裂点需使下式取得最小值：

$M S E (R_{k l}) \times \frac{N_{k l}}{N_{k}} + M S E (R_{k r}) \times \frac{N_{k r}}{N_{k}} (2)$

其中， $N_{k}$ 、 $N_{k l}$ 和 $N_{k r}$ 分别代表节点 $R_{k}$ 、 $R_{k l}$ 和 $R_{k r}$ 中的观察单位数量。

树的剪枝

对由CART生成的回归树的剪枝使用的方法称为代价复杂性剪枝；该方法首先从训练集通过上述过程形成一棵完整的决策树 $T_{0}$ ，然后再去除于某些内部节点上形成的分支进而得到剪枝后的子树 $T$ ，属于后剪枝³。记控制树的复杂度的超参数为 $α$ （ $α \geq 0$ ），代价复杂性剪枝所找到的子树 $T$ 需使下式获得最小值：

³ 与预剪枝相比，后剪枝通常对树保留更多的分支，使其欠拟合风险小，且泛化性能往往优于预剪枝；但其训练时间更长。

$C_{α} (T) = \sum_{k = 1}^{m} M S E (R_{k}) \times N_{k} + α m (3)$

其中， $m$ 为子树 $T$ 所含的叶节点个数； $N_{k}$ 为位于叶节点 $R_{k}$ 中的观察单位个数。显而易见，当 $α = 0$ 时，相当于保留完整的树； $α$ 越大，所得到的数的分支越少。超参数 $α$ 的最优值可以通过交叉验证等重抽样方法确定；以下进一步介绍给定 $α$ 时子树的选取规则。

剪枝的过程从下往上进行。遍历所有内部节点⁴，选择其中一个去除，使 $\sum_{k = 1}^{m} M S E (R_{k}) \times N_{k}$ 增幅最小；对所得子树重复该过程，直至所得子树只剩下根节点。该过程形成了一系列子树；可以证明，使式(3)中 $C_{a} (T)$ 取得最小值的子树就位于其中。因此，最后只需通过比较该系列子树的 $C_{a} (T)$ 值，即可得到目标子树。

⁴ 一般是叶节点的父节点。

一个疑问

在写作本文时，我对递归二分裂与代价复杂性剪枝间的关系产生了一个疑问：假设递归二分裂过程中形成的一系列树的集合为 $T_{r}$ ，再假设代价复杂性剪枝过程中形成的一系列树的集合为 $T_{p}$ ，那么 $T_{r}$ 是否等价于 $T_{p}$ ？如果两者等价，那么在进行递归二分裂的过程中即可记录式(3)中的 $C_{α} (T)$ 值，并在完整决策树形成后即可直接选出最优子树，而无需再进行代价复杂性剪枝了。

该问题可以借助图 2 进行分析。可以发现，只有当递归二分裂过程中形成的分裂点的顺序正好与代价复杂性剪枝过程中合并的分裂点的顺序相反时， $T_{p}$ 才等价于 $T_{r}$ ；在其他情况下，两者并不等价。