指数加权移动均值的计算方法及代码实现
本文主要介绍了一种指数加权移动均值的计算方法，并给出了一些计算示例。另外，本文还提供了所述算法的SQL和R语言代码实现。
引言
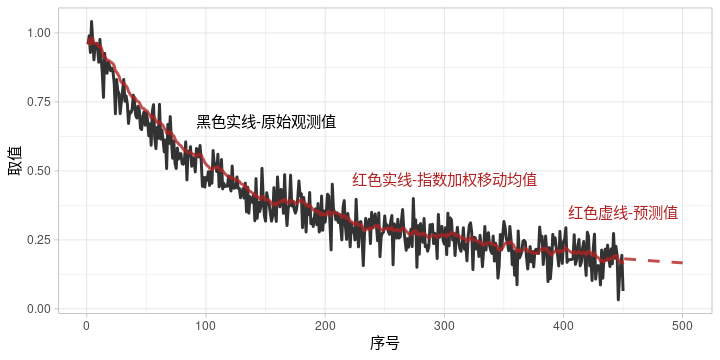
指数加权移动均值（Exponentially Weighted Moving Average, EWMA）是一种计算有序序列的加权均值的统计学方法。该方法可以根据各个观测值在序列中的位置分配呈指数变化的权重，使得序列中越靠后的观测值对计算结果的影响越大；并且，它还可以通过参数调节权重的变化幅度。由于具有这些特性，指数加权移动均值相对于常规的算术均值、加权均值和移动均值，更加适用于解决时间序列相关问题，例如：
1 常用于时间序列预测的指数平滑模型 (ETS模型)，就是基于指数加权移动均值设计的。
但另一方面，指数加权移动均值的计算方法却比较复杂、现成的程序实现也并不多见，使得其日常应用比较受限。针对这些问题，本文将对该算法进行详细介绍，同时还将结合具体的例子给出算法的SQL和R语言代码实现；所提供的代码除了可以直接使用外，也可以作为参考材料指导读者在其他编程语言中实现该算法。
计算方法
以\(x\)表示一条序列、\(t\)表示序列中观测值的序号，并且以\(w\)表示一个给定的权重调节参数、以\(x_0\)表示一个给定的序列初始值，那么与\(t\)对应的序列\(x\)的指数加权移动均值\(\bar{x}_t\)可以表示为 定义 1 ：
定义 1 \[ \begin{cases} \begin{align} \bar{x}_1 &= (1 - w) x_0 + w x_1, \quad &t = 1 \\ \bar{x}_{t} &= (1 - w) \bar{x}_{t-1} + w x_t, \quad &t = 2, ..., T \end{align} \end{cases} \]
若是递归地对 定义 1 右侧所含的指数加权移动平均项\((\bar{x}_{t-1}, \bar{x}_{t-2}, ...)\)进行分解和代入，那么\(\bar{x}_t\)也可以表示为 定义 2 ：
定义 2 \[ \bar{x}_{t} = (1 - w)^t x_0 + \sum_{i = 0}^{t - 1} w (1 - w)^i x_{t - i}, \quad t = 1, ..., T \]
假设\(x_0 = 0\)，那么\(\bar{x}_{t}\)就是原序列\(x\)中前\(t\)个时间点的加权均值，且各项权重能够组成一个以\(w\)为首项、\(1 - w\)为比、\(t\)为项数的等比数列\(a_t = w(1 - w)^{t - 1}\)；而根据等比数列求和公式，可知权重之和为\(S_t = 1 - (1 - w)^t\)。由于\(0 < 1 - w < 1\)，所以\(S_t < 1\)恒成立，且\(t\)越小则\(S_t\)与1的差值越大。这意味着，在按照 定义 1 或 定义 2 计算移动均值时，由于各项权重之和小于1，最终所得结果的绝对值会偏小。
为了对上述偏差进行校正，可以将\(\bar{x}_{t}\)除以\(S_t\)，以便使权重之和恒等于1。如果以\(\bar{x}^{'}_{t}\)表示校正后的指数加权均值，则有 定义 3 ：
定义 3 \[ \bar{x}^{'}_{t} = \frac{\bar{x}_t}{1 - (1 - w)^t} \]
有了以上校正方法，即使参与计算的序列观测值个数比较少，结果也不会有太大的误差。因此，在计算截至序列某点（\(t=T\)）的指数加权移动均值时，可以不再使用从序列起点至该点（\(t=1\)至\(t=T\)）的所有观测值、而改用更小的移动窗口（例如，\(t=T-4\)至\(t=T\)）；对某些程序实现来说，这样可以减少计算量和计算时间。
参数意义
定义 1 / 定义 2 中的\(x_0\)和\(w\)都属于可以调节的参数，能够影响计算的结果。在指数加权移动均值的某些应用场景中（例如，机器学习特征工程），可以预先给出多个不同的参数取值、然后通过交叉验证来确定最合适的参数值；在另一些应用场景中，使用者可能希望直接设定参数的取值、让结果更加直观和可解释。对于后者来说，正确理解参数意义是重要前提。下面将分别介绍\(x_0\)和\(w\)的意义和取值建议。
\(x_0\)的意义最主要是提高算法的完整性和连贯性；除此以外，也能在一定程度上用于校正前面讲到的偏差。但是由于 定义 3 的校正效果更好，因此多数情况下宜令\(x_0 = 0\)。
如果\(x_0 = 0\)，那么根据 定义 2 ，可知\(x_{t - i}\)（\(t - i > 0\)）的权重与\(x_t\)的权重之比为\((1 - w)^i\)。数学上可以证明，对于任意\(0 < w < 1\)，均有\((1 - w)^{\frac{1}{w}} < \frac{1}{e} \approx 0.37\)。如果把\(0.37\)视作一个临界值、且当\(x_{t-i}\)与\(x_t\)的权重之比小于该临界值时，\(t - i\)至\(1\)的观测值对总体移动均值的影响可以忽略；那么，因为\(i \geq \frac{1}{w}\)时\((1 - w)^i < 0.37\)恒成立，所以可以认为指数加权移动均值主要代表的就是序列中靠近末尾的\(\frac{1}{w}\)个观测值的集中程度。也就是说，参数\(w\)的倒数代表了对指数加权移动均值结果影响最大的末尾观测值个数；但需要注意的是，这只是一种经验性的理解 (Ng 2018) 。
根据上面的理解，对于\(x_0\)来说，在实际应用中通常可以取\(x_0 = 0\)，并且再在此基础上对结果进行校正；而至于\(w\)，如果业务需求主要考虑序列末尾\(k\)个观察值的影响，那么可以取\(w = \frac{1}{k}\)。
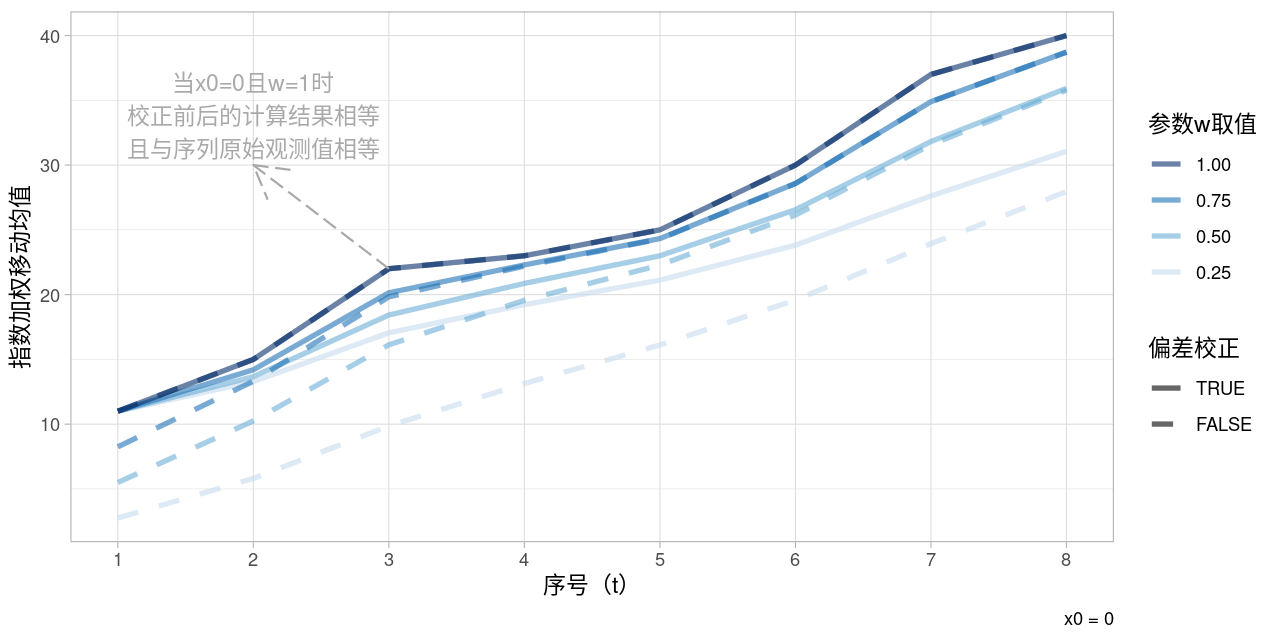
图 2 直观地展示了参数\(w\)取值以及偏差校正对计算结果的影响（所用数据为下文所提供的信号A样例数据；并且计算时假设\(x_0 = 0\)）。从图中可以看出：1. 相对于校正后的结果，校正前的结果的绝对值偏小，且该偏差会随着\(w\)或序号\(t\)的减小而增加；2. 在\(0 < w < 1\)范围内，校正前后的指数加权移动均值会随着\(w\)的增大而更加接近序列原始观测值，且当\(w = 1\)时三者完全重合。
SQL代码实现及示例
本文将以PostgreSQL为例给出有关代码 2 并进行讲解。
2 这些代码在PostgreSQL 15.4中测试通过。
由于实际应用时，往往需要同时对多组序列计算指数加权移动均值；因此，为了提高参考价值，下面将使用含有多组序列的样例数据。
假设表xt保存了由信号A和信号B的观测值分别组成的序列，且该表的具体定义及所含数据如下：
CREATE TEMPORARY TABLE xt (
signal VARCHAR, -- 信号标识
t INT, -- 观测值序号
x DOUBLE PRECISION -- 观测值大小
);
INSERT INTO xt
VALUES ('A', 1, 11.0), ('B', 1, 13.0),
('A', 2, 15.0), ('B', 2, 19.0),
('A', 3, 22.0), ('B', 3, 20.0),
('A', 4, 23.0), ('B', 4, 22.0),
('A', 5, 25.0), ('B', 5, 26.0),
('A', 6, 30.0), ('B', 6, 32.0),
('A', 7, 37.0), ('B', 7, 34.0),
('A', 8, 40.0);如果以代码变量x0代表算法参数\(x_0\)、变量w代表参数\(w\)、以变量correct_bias表示是否对偏差进行校正，再假设x0 = 0、w = 0.25、correct_bias = TRUE，那么基于 定义 1 和 定义 3 （下称方法1）、以及基于 定义 2 和 定义 3 （下称方法2）的两种指数加权移动均值计算方法实现如下所示：
DO $$
DECLARE
x0 DOUBLE PRECISION := 0;
w DOUBLE PRECISION := 0.25;
correct_bias BOOLEAN := TRUE;
BEGIN
-- 方法1：对应定义1和定义3
CREATE TEMPORARY TABLE result_1 AS
WITH RECURSIVE ta AS (
SELECT CAST(NULL AS VARCHAR) AS signal,
CAST(0 AS INT) AS t,
CAST(x0 AS DOUBLE PRECISION) AS x
UNION ALL
SELECT tb.signal, tb.t AS t, (1 - w) * ta.x + w * tb.x AS x
FROM ta
INNER JOIN xt AS tb ON (ta.signal IS NULL OR ta.signal = tb.signal) AND ta.t + 1 = tb.t
)
SELECT signal, t, x / CASE WHEN correct_bias THEN (1 - (1 - w) ^ t) ELSE 1 END AS x
FROM ta
WHERE t >= 1
ORDER BY signal, t;
-- 方法2：对应定义2和定义3
CREATE TEMPORARY TABLE result_2 AS
SELECT signal, t, (sum(w * x * (1 - w) ^ i) + (1 - w) ^ t * x0) / CASE WHEN correct_bias THEN (1 - (1 - w) ^ t) ELSE 1 END AS x
FROM (SELECT ta.signal, ta.t AS t, ta.t - tb.t AS i, tb.x
FROM xt AS ta
INNER JOIN xt AS tb ON ta.signal = tb.signal
WHERE ta.t >= tb.t) ta
GROUP BY signal, t
ORDER BY signal, t;
END $$;表格 1 给出了计算结果（基于两种方法的计算结果相同）：
| signal | t | x |
|---|---|---|
| A | 1 | 11.0 |
| A | 2 | 13.3 |
| A | 3 | 17.1 |
| A | 4 | 19.2 |
| A | 5 | 21.1 |
| A | 6 | 23.8 |
| A | 7 | 27.6 |
| A | 8 | 31.1 |
| B | 1 | 13.0 |
| B | 2 | 16.4 |
| B | 3 | 18.0 |
| B | 4 | 19.4 |
| B | 5 | 21.6 |
| B | 6 | 24.8 |
| B | 7 | 27.4 |
值得一提的是，尽管两种计算方法实现所得的最终结果相同，但它们存在一些功能要求和性能上的差异：
- 基于方法1的SQL实现需要用到递归查询，但并非所有数据库管理系统支持该功能，因此可移植性并不如基于方法2的实现；
- 两者在计算速度上往往具有差异，且在不同情况下优势可以互换 3 。
3 简单的测试结果提示，当序列观察值个数（本例中字段t的唯一值个数）较多时，基于方法1的实现可能更高效；当序列分组个数（本例中字段signal的唯一值个数）较多时，则基于方法2的实现可能更高效。
R语言代码实现及示例
下面给出的ewma()函数可以用于计算校正后的指数加权移动均值，其中参数x为原始序列数据、参数w为指数加权的权重、参数x0为序列的初始值、参数correct_bias代表是否校正偏差；与前例类似，这里分别给出基于 定义 1 和 定义 3 （方法1）、以及基于 定义 2 和 定义 3 （方法2）的代码实现（两者的计算结果相同，但性能存在差异）：
# 方法1：对应定义1和定义3
# 绝大多数情况下计算速度较快，推荐使用
ewma <- function(x, w = 0.25, x0 = 0, correct_bias = TRUE) {
result <- Reduce(function(xt_1, xt) {
(1 - w) * xt_1 + w * xt
}, x = x, accumulate = T, init = x0)[-1]
if (correct_bias) {
t <- seq_along(x)
result <- result / (1 - (1 - w) ^ t)
}
result
}
# 方法2：对应定义2和定义3
# 绝大多数情况下计算速度较慢，不推荐使用
# ewma <- function(x, w = 0.25, x0 = 0, correct_bias = TRUE) {
# result <- vapply(seq_along(x), function(t) {
# i <- seq_len(t)
# (1 - w) ^ t * x0 + sum(x[i] * w * (1 - w) ^ (t - i))
# }, double(1))
# if (correct_bias) {
# t <- seq_along(x)
# result <- result / (1 - (1 - w) ^ t)
# }
# result
# }下面将前例中信号A的数据赋值给向量xt，并仅以该数据演示计算结果：
xt <- c(11.0, 15.0, 22.0, 23.0, 25.0, 30.0, 37.0, 40.0)以下是利用函数ewma()算出的校正前和校正后的指数加权移动均值：
# 校正前
ewma(xt, w = 0.25, x0 = 0, correct_bias = FALSE)[1] 2.8 5.8 9.9 13.1 16.1 19.6 23.9 28.0# 校正后
ewma(xt, w = 0.25, x0 = 0, correct_bias = TRUE)[1] 11.0 13.3 17.1 19.2 21.1 23.8 27.6 31.1